Class for stock-recruitment models.
Usage
FLSR(model, ...)
# S4 method for class 'ANY'
FLSR(model, ...)
# S4 method for class 'missing'
FLSR(model, ...)Details
A series of commonly-used stock-recruitment models are already available,
including the corresponding likelihood functions and calculation of initial
values. See SRModels for more details and the exact
formulation implemented for each of them.
Slots
- name
Name of the object (
character).- desc
Description of the object (
character).- range
Range (
numeric).- rec
Recruitment series (
FLQuant).- ssb
Index of reproductive potential, e.g. SSB or egg oor egg production (
FLQuant).- fitted
Estimated values for rec (
FLQuant).- residuals
Residuals obtained from the model fit (
FLArray).- covar
Covariates for SR model (
FLQuants).- model
Model formula (
formula).- gr
Function returning the gradient of the likelihood (
function).- logl
Log-likelihood function (
function).- initial
Function returning initial parameter values for the optimizer (
function).- params
Estimated parameter values (
FLPar).- logLik
Value of the log-likelihood (
logLik).- vcov
Variance-covariance matrix (
array).- details
Extra information on the model fit procedure (
list).- logerror
Is the error on a log scale (
logical).- distribution
(
factor).- hessian
Resulting Hessian matrix from the fit (
array).
Examples
# Create an empty FLSR object.
sr1 <- FLSR()
# Create an FLSR object using the existing SR models.
sr2 <- FLSR(model = 'ricker')
sr2@model
#> rec ~ a * ssb * exp(-b * ssb)
#> <environment: 0x55d3726ebde0>
sr2@initial
#> function(rec, ssb) {
#> # The function to provide initial values
#> res <-coefficients(lm(log(c(rec)/c(ssb))~c(ssb)))
#> return(FLPar(a=max(exp(res[1])), b=-max(res[2])))}
#> <bytecode: 0x55d3726e6550>
#> <environment: 0x55d3726ebde0>
#> attr(,"lower")
#> [1] -Inf -Inf
#> attr(,"upper")
#> [1] Inf Inf
sr2@logl
#> function(a, b, rec, ssb)
#> loglAR1(log(rec), log(a*ssb*exp(-b*ssb)))
#> <bytecode: 0x55d3726e4c50>
#> <environment: 0x55d3726ebde0>
sr3 <- FLSR(model = 'bevholt')
sr3@model
#> rec ~ a * ssb/(b + ssb)
#> <environment: 0x55d372ad2e30>
sr3@initial
#> function(rec, ssb) {
#> a <- max(quantile(c(rec), 0.75, na.rm = TRUE))
#> b <- max(quantile(c(rec)/c(ssb), 0.9, na.rm = TRUE))
#> return(FLPar(a = a, b = a/b))}
#> <bytecode: 0x55d372acbed0>
#> <environment: 0x55d372ad2e30>
#> attr(,"lower")
#> [1] -Inf -Inf
#> attr(,"upper")
#> [1] Inf Inf
sr3@logl
#> function(a, b, rec, ssb)
#> loglAR1(log(rec), log(a*ssb/(b+ssb)))
#> <bytecode: 0x55d372aca560>
#> <environment: 0x55d372ad2e30>
# Create an FLSR using a function.
mysr1 <- function(){
model <- rec ~ a*ssb^b
return(list(model = model))}
sr4 <- FLSR(model = mysr1)
# Create an FLSR using a function and check that it works.
mysr2 <- function(){
formula <- rec ~ a+ssb*b
logl <- function(a, b, sigma, rec, ssb) sum(dnorm(rec,
a + ssb*b, sqrt(sigma), TRUE))
initial <- structure(function(rec, ssb) {
a <- mean(rec)
b <- 1
sigma <- sqrt(var(rec))
return(list(a=a, b=b, sigma=sigma))},
lower = c(0, 1e-04, 1e-04), upper = rep(Inf, 3))
return(list(model = formula, initial = initial, logl = logl))
}
ssb <- FLQuant(runif(10, 10000, 100000))
rec <- 10000 + 2*ssb + rnorm(10,0,1)
sr5 <- FLSR(model = mysr2, ssb = ssb, rec = rec)
sr5.mle <- fmle(sr5)
#> Nelder-Mead direct search function minimizer
#> function value for initial parameters = 262595.385209
#> Scaled convergence tolerance is 0.00391298
#> Stepsize computed as 10445.153925
#> BUILD 4 28645452399358.968750 221224.646488
#> LO-REDUCTION 6 6546657876347.041016 221224.646488
#> HI-REDUCTION 8 1659966262080.467773 221224.646488
#> HI-REDUCTION 10 417829373222.549988 221224.646488
#> HI-REDUCTION 12 104746515448.884705 221224.646488
#> HI-REDUCTION 14 26188278994.874119 221224.646488
#> HI-REDUCTION 16 6530003680.701155 221224.646488
#> HI-REDUCTION 18 1621814816.285557 221224.646488
#> HI-REDUCTION 20 399931604.523688 221224.646488
#> HI-REDUCTION 22 97289980.805041 221224.646488
#> HI-REDUCTION 24 23075088.181383 221224.646488
#> HI-REDUCTION 26 5247988.802065 221224.646488
#> HI-REDUCTION 28 1155009.339887 221224.646488
#> HI-REDUCTION 30 360708.942755 221224.646488
#> REFLECTION 32 313722.608957 184489.369857
#> HI-REDUCTION 34 262595.385209 184489.369857
#> LO-REDUCTION 36 221224.646488 171120.002924
#> HI-REDUCTION 38 192087.923302 157925.622884
#> EXTENSION 40 184489.369857 108699.474779
#> LO-REDUCTION 42 171120.002924 108699.474779
#> LO-REDUCTION 44 157925.622884 108699.474779
#> EXTENSION 46 128070.906599 76101.388372
#> EXTENSION 48 119152.983479 64476.917526
#> LO-REDUCTION 50 108699.474779 64476.917526
#> LO-REDUCTION 52 86152.658342 64476.917526
#> EXTENSION 54 76101.388372 36020.404937
#> LO-REDUCTION 56 67550.265570 36020.404937
#> EXTENSION 58 64476.917526 27777.915928
#> EXTENSION 60 46071.299646 2038.886066
#> LO-REDUCTION 62 36020.404937 2038.886066
#> LO-REDUCTION 64 27777.915928 2038.886066
#> LO-REDUCTION 66 17800.207184 2038.886066
#> REFLECTION 68 9768.507415 1117.922206
#> LO-REDUCTION 70 2568.549432 584.825923
#> LO-REDUCTION 72 2038.886066 584.825923
#> HI-REDUCTION 74 1117.922206 216.128761
#> HI-REDUCTION 76 593.382359 216.128761
#> LO-REDUCTION 78 584.825923 216.128761
#> LO-REDUCTION 80 390.983431 92.041933
#> HI-REDUCTION 82 268.849591 92.041933
#> HI-REDUCTION 84 216.128761 92.041933
#> HI-REDUCTION 86 151.128805 81.710051
#> HI-REDUCTION 88 114.341919 81.710051
#> LO-REDUCTION 90 93.833844 80.444305
#> HI-REDUCTION 92 92.041933 73.432910
#> LO-REDUCTION 94 81.710051 73.432910
#> REFLECTION 96 80.444305 72.722277
#> LO-REDUCTION 98 73.739358 71.444740
#> HI-REDUCTION 100 73.432910 69.352884
#> REFLECTION 102 72.722277 68.919394
#> LO-REDUCTION 104 71.444740 68.919394
#> HI-REDUCTION 106 69.510860 68.919394
#> HI-REDUCTION 108 69.352884 68.919394
#> HI-REDUCTION 110 69.049015 68.919394
#> LO-REDUCTION 112 68.995222 68.919394
#> HI-REDUCTION 114 68.957692 68.916139
#> HI-REDUCTION 116 68.919970 68.907335
#> HI-REDUCTION 118 68.919394 68.901648
#> HI-REDUCTION 120 68.916139 68.901250
#> LO-REDUCTION 122 68.907335 68.901250
#> Exiting from Nelder Mead minimizer
#> 124 function evaluations used
sr5.nls <- nls(sr5)
# NS Herring stock-recruitment dataset
data(nsher)
# already fitted with a Ricker SR model
summary(nsher)
#> An object of class "FLSR"
#>
#> Name:
#> Description:
#> Quant: age
#> Dims: age year unit season area iter
#> 1 45 1 1 1 1
#>
#> Range: min minyear max maxyear
#> 0 1960 0 2004
#>
#>
#> Model: rec ~ a * ssb * exp(-b * ssb)
#> An object of class "FLPar"
#> params
#> a b
#> 1.19e+02 9.45e-03
#> units: NA
#> Log-likelihood: 15.862(0)
#> Variance-covariance:
#> a b
#> a 255.3388181 1.808870e-02
#> b 0.0180887 1.992659e-06
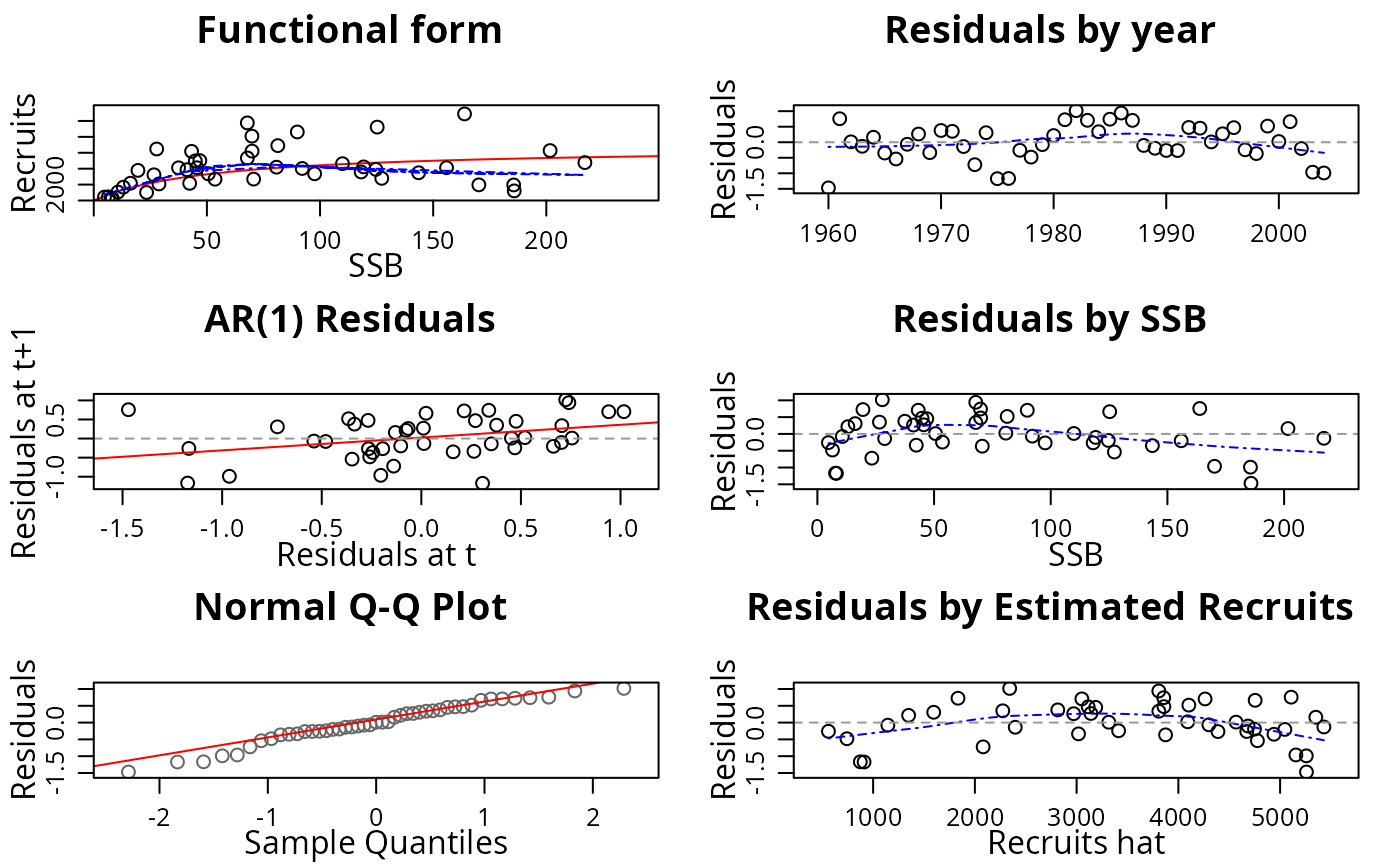
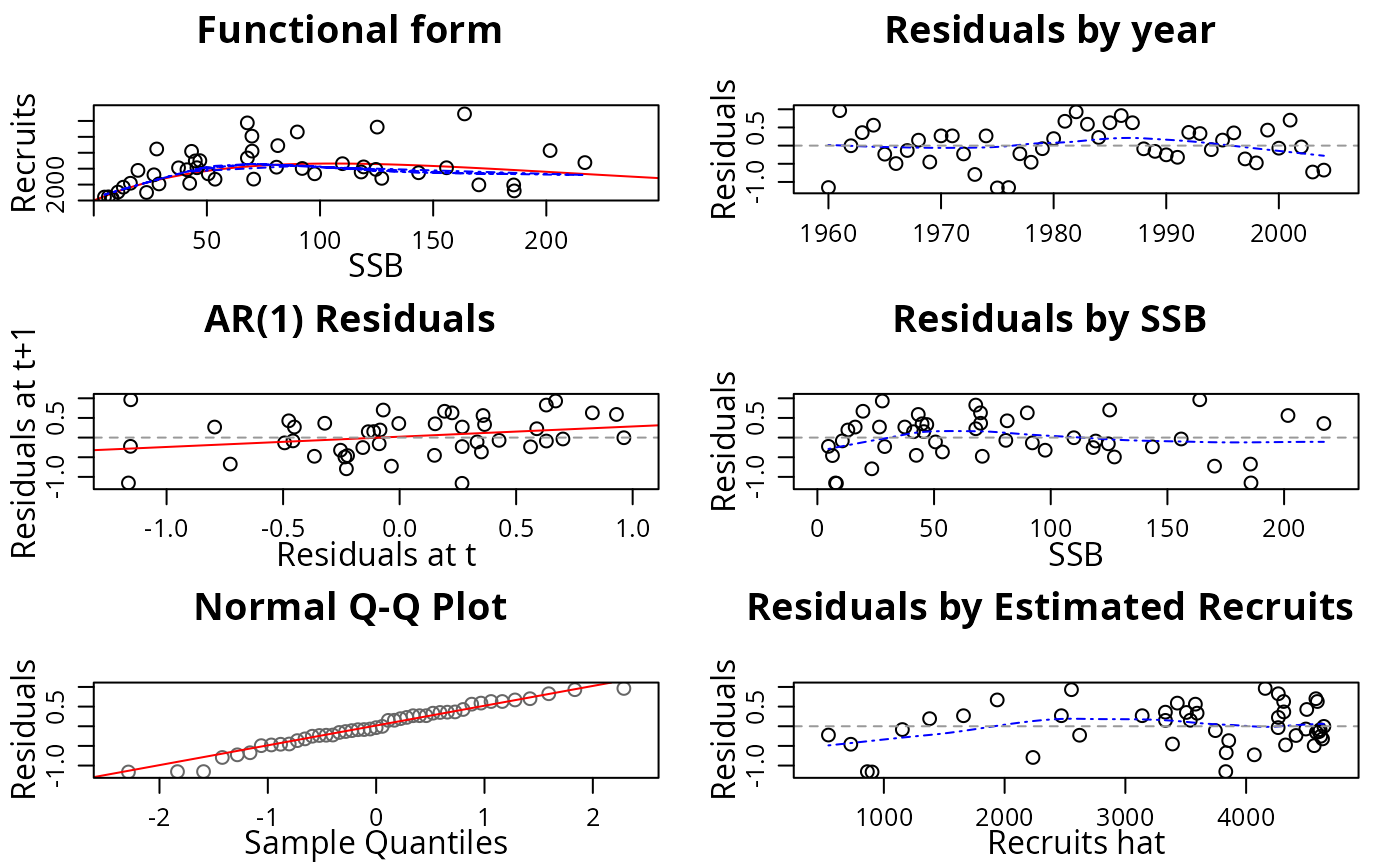
plot(nsher)
# change model
model(nsher) <- bevholt()
# fit through MLE
nsher <- fmle(nsher)
#> Nelder-Mead direct search function minimizer
#> function value for initial parameters = -10.336211
#> Scaled convergence tolerance is 1.54022e-07
#> Stepsize computed as 501.110000
#> BUILD 3 44.842344 -11.603908
#> Warning: NaNs produced
#> HI-REDUCTION 5 31.685209 -11.603908
#> Warning: NaNs produced
#> HI-REDUCTION 7 17.913114 -11.603908
#> Warning: NaNs produced
#> HI-REDUCTION 9 5.415279 -11.603908
#> Warning: NaNs produced
#> HI-REDUCTION 11 -3.412974 -11.603908
#> HI-REDUCTION 13 -8.018030 -11.603908
#> LO-REDUCTION 15 -10.336211 -11.603908
#> LO-REDUCTION 17 -11.081040 -11.603908
#> EXTENSION 19 -11.295930 -12.061705
#> LO-REDUCTION 21 -11.603908 -12.061705
#> REFLECTION 23 -11.813826 -12.087620
#> REFLECTION 25 -12.061705 -12.199591
#> LO-REDUCTION 27 -12.087620 -12.199591
#> LO-REDUCTION 29 -12.158184 -12.199591
#> LO-REDUCTION 31 -12.191726 -12.199591
#> HI-REDUCTION 33 -12.192269 -12.199591
#> HI-REDUCTION 35 -12.197784 -12.199591
#> LO-REDUCTION 37 -12.198015 -12.199591
#> HI-REDUCTION 39 -12.199555 -12.199776
#> REFLECTION 41 -12.199591 -12.200058
#> HI-REDUCTION 43 -12.199776 -12.200092
#> HI-REDUCTION 45 -12.200058 -12.200142
#> HI-REDUCTION 47 -12.200092 -12.200155
#> HI-REDUCTION 49 -12.200142 -12.200160
#> HI-REDUCTION 51 -12.200155 -12.200177
#> HI-REDUCTION 53 -12.200160 -12.200177
#> LO-REDUCTION 55 -12.200171 -12.200179
#> HI-REDUCTION 57 -12.200177 -12.200179
#> HI-REDUCTION 59 -12.200178 -12.200179
#> HI-REDUCTION 61 -12.200179 -12.200179
#> HI-REDUCTION 63 -12.200179 -12.200179
#> HI-REDUCTION 65 -12.200179 -12.200179
#> Exiting from Nelder Mead minimizer
#> 67 function evaluations used
plot(nsher)
